Modeling of the hadron-to-quark surface tension and its imprints in neutron star observations
Prepared by Tianqi Zhao and Sophia Han
When ordinary matter such as water is heated up or compressed, the atoms reconfigure themselves and a range of intriguing phases — solid (ice), liquid (water), and gas (vapor) — will emerge under different conditions. At exceedingly high densities and temperatures in the cores of ultra-compact celestial bodies like neutron stars, the dense, compressed nuclear matter mainly consisting of baryons (protons and neutrons) and leptons (electrons and muons) may undergo mysterious transformations, giving rise to exotic phases of quark matter. The precise density at which this phase shift takes place, as well as the associated surface tension at the hadron-to-quark phase boundary, remains enigmatic.
A significant astrophysical implication hinges on this critical density: if it occurs below the central density of a neutron star (approximately ![]() grams per cubic centimeter depending on its mass), these “hybrid” stars possess an exotic matter core; otherwise, they remain entirely hadronic. Fortunately our observation tools, including X-ray telescopes, neutrino detectors, and gravitational-wave observatories, allow us to investigate neutron stars and potentially uncover the secrets of this phase transition. Such investigations promise profound insights into quantum chromodynamics (QCD), the fundamental theory of strong interactions.
grams per cubic centimeter depending on its mass), these “hybrid” stars possess an exotic matter core; otherwise, they remain entirely hadronic. Fortunately our observation tools, including X-ray telescopes, neutrino detectors, and gravitational-wave observatories, allow us to investigate neutron stars and potentially uncover the secrets of this phase transition. Such investigations promise profound insights into quantum chromodynamics (QCD), the fundamental theory of strong interactions.
In our latest study, we introduce a novel framework designed to model the transition from hadronic matter to quark matter considering various levels of the surface tension. To better understand the role of surface tension, imagine the interface between water and air: when detergent is added into water, the surface tension diminishes, enabling thicker foams to form and remain stable. In the case of the hadron-to-quark phase transition in the interior of neutron stars, we encounter similar phenomena but on a cosmic scale. Here, assuming infinite surface tension leads to a clean separation of two bulk phases, treated quantitatively by what is known as the Maxwell construction, while zero surface tension results in a foam-like mixture known as the Gibbs construction. For intermediate values of the surface tension, we must engage in intricate calculations involving Coulomb and surface energy within Wigner-Seitz cells of varying geometries to determine the most stable configuration with the lowest energy. This configuration can resemble spherical droplets in three dimensions, spaghetti in two dimensions, or lasagna in one dimension, often whimsically referred to as the “pasta” phase.
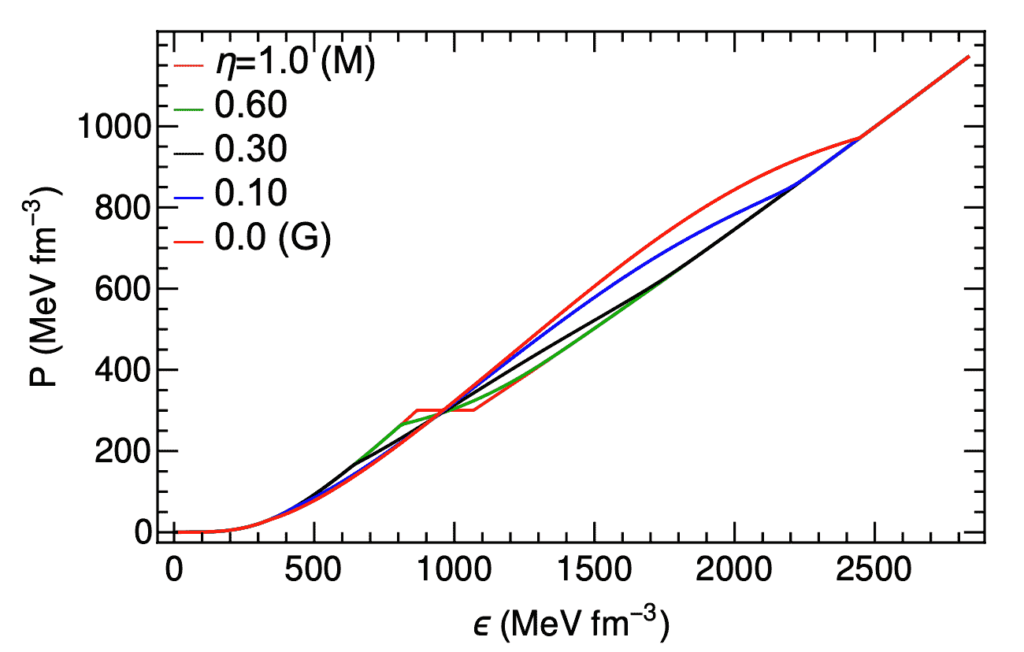
To simplify, we introduce a parameter denoted as η (ranging from 0 to 1) to serve as a proxy for the surface tension, allowing us to navigate between the Maxwell and Gibbs constructions. This approach facilitates the calculation of the equation of state and the chemical composition of matter within the transitional phase region. Figure 1 illustrates how varying η affects the equation of state in the pressure versus energy-density plane for the hadron-to-quark phase transition. When η=1, it corresponds to the Maxwell construction with a sharp density discontinuity, whereas η=0 corresponds to the Gibbs construction, fully mixing the two phases.
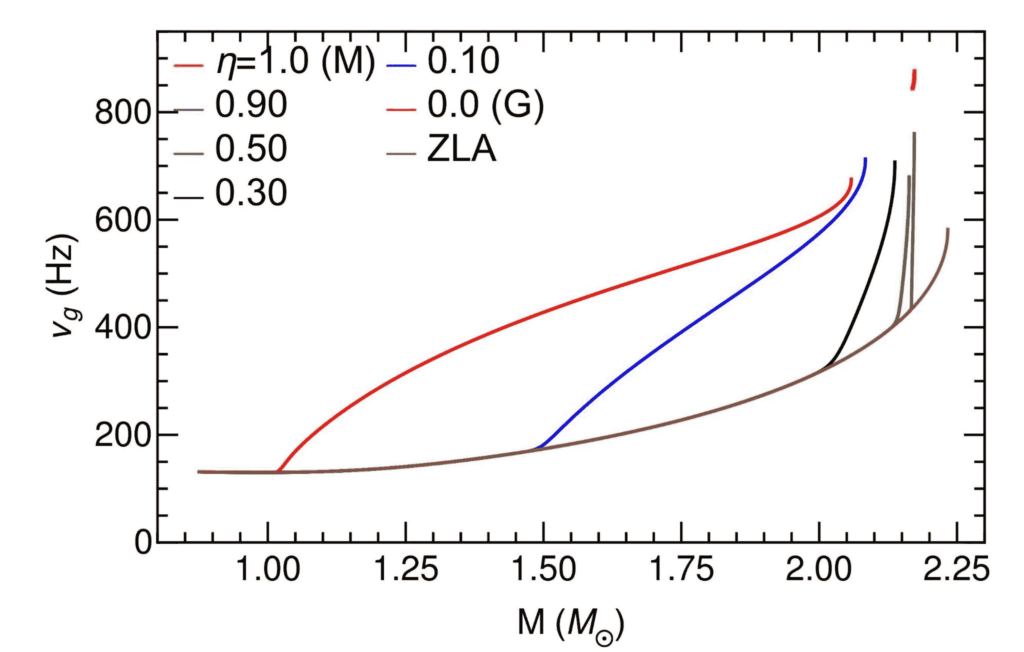
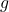 -mode frequency ν_g as a function of the neutron star mass M. The rapid rise in ν_g occurs at progressively higher densities with larger η and is increasingly steeper. Note that the small orange line segment above 800 Hz corresponds to the discontinuity
-mode frequency ν_g as a function of the neutron star mass M. The rapid rise in ν_g occurs at progressively higher densities with larger η and is increasingly steeper. Note that the small orange line segment above 800 Hz corresponds to the discontinuity 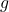 -mode of the Maxwell construction.
-mode of the Maxwell construction. Regarding astrophysical implications, our research in particular delves into how the level of surface tension would affect the characteristic frequencies of neutron stars’ ![]() -mode (gravity mode) vibrations; such oscillation modes are expected to be identified and extracted from future gravitational-wave events of e.g. merging neutron stars through sophisticated waveform analysis. Figure 2 showcases our predictions for the
-mode (gravity mode) vibrations; such oscillation modes are expected to be identified and extracted from future gravitational-wave events of e.g. merging neutron stars through sophisticated waveform analysis. Figure 2 showcases our predictions for the ![]() -mode frequency ν_g, as the η parameter varies within the range of 0 to 1. Ideally, with sufficient observations of these
-mode frequency ν_g, as the η parameter varies within the range of 0 to 1. Ideally, with sufficient observations of these ![]() -mode oscillations, one can infer the unknown onset density and surface tension magnitude associated with the phase transition from hadronic matter to quark matter.
-mode oscillations, one can infer the unknown onset density and surface tension magnitude associated with the phase transition from hadronic matter to quark matter.
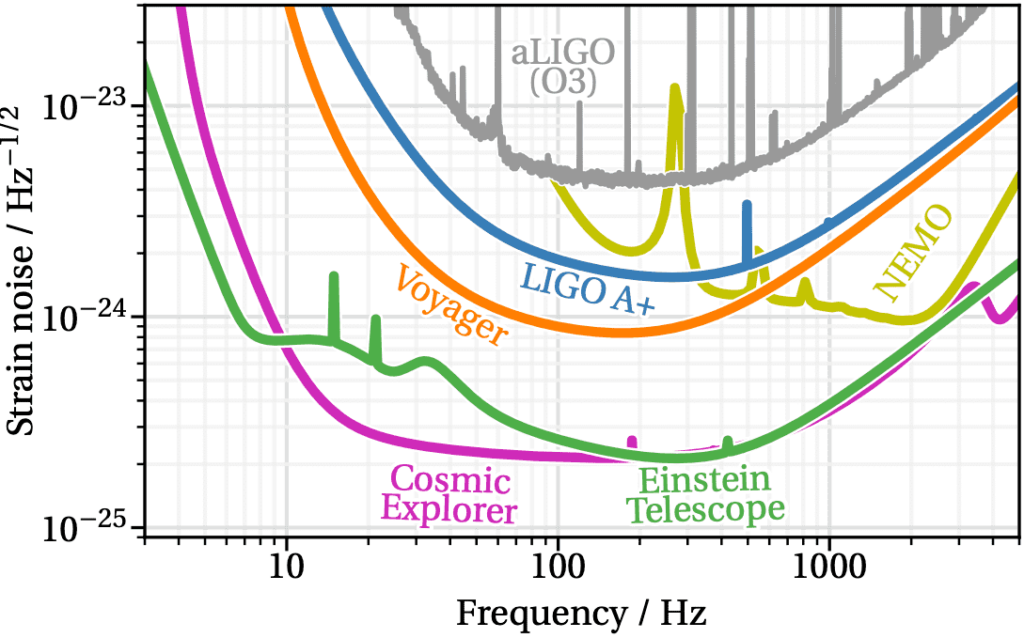
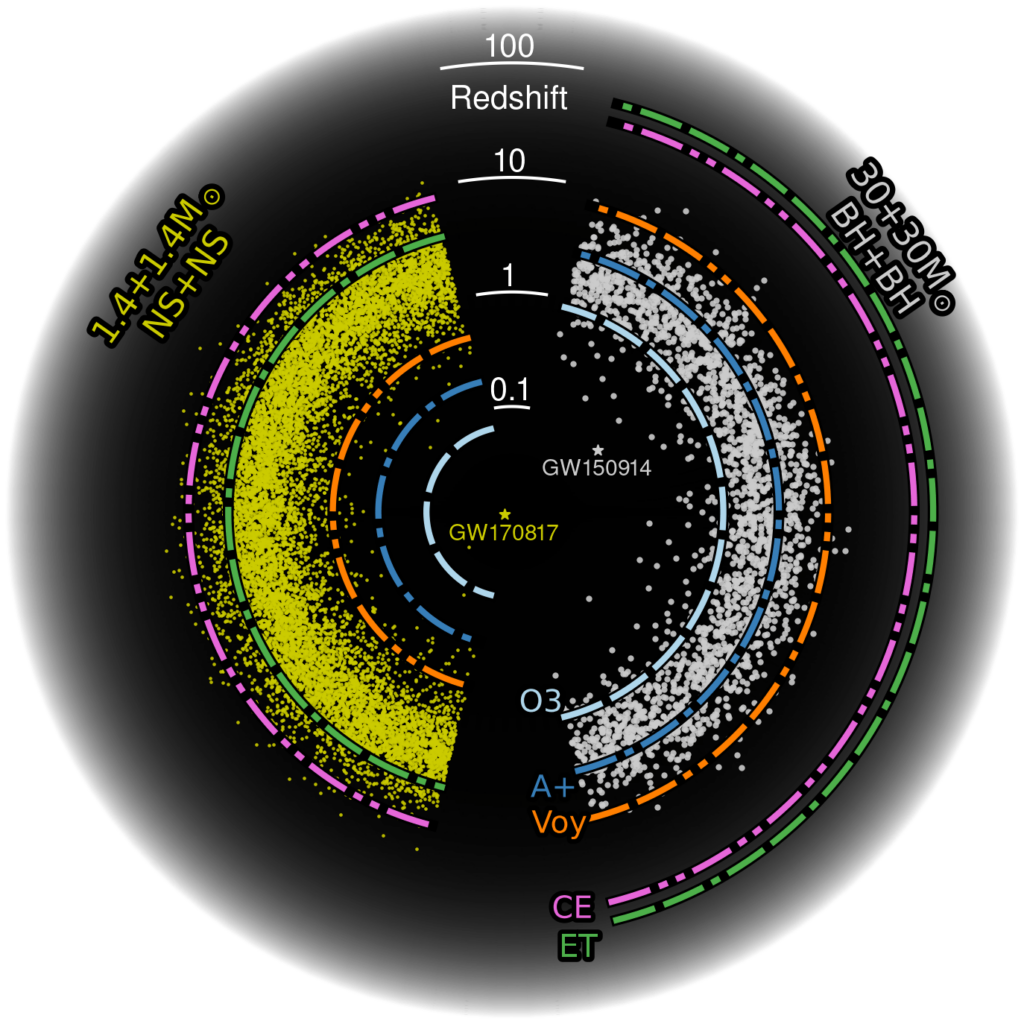
Although current gravitational-wave observatories such as LIGO-Virgo-KAGRA still lack the required sensitivity to detect these subtle signals so far, next generation detectors including the Cosmic Explorer in the United States and the Einstein Telescope in the European Union (see Figure 3) will offer opportunities with necessary data and increasingly better resolution to shed light on this unsolved mystery about the phase structure inside neutron stars. These advanced instruments could open a new chapter to greatly enhance our understanding of the fundamental forces that govern the behavior of matter under extreme conditions in the Universe.
Header image: Astrophysical horizon of current and proposed future gravitational-wave detectors for compact binary systems of neutron stars and black holes. Credit: Cosmic Explorer Project
Read More: